Ensure you have a strong grasp of the Pearson alternative text general guidelines before starting any alt text project.
Pearson uses the principles of MathSpeak when authoring alternative text for images containing STEM content. Using MathSpeak grammar rules provides students with print disabilities a description of what would be naturally spoken in the classroom and does not overwhelm them with information that is not needed to understand the content.
The following topics address guidance when authoring image descriptions:
When working in the MathXL space, also review Section 8.1 Alt Text which is an excerpt of the MathXL Content Standards & Development Guidelines.
Numbers and Dates
- Cardinal numbers (1, 2, 3, 4…) – are announced correctly by screen readers. Numbers can stay as cardinal numbers.
- Ordinal numbers (1st, 2nd, 3rd, 4th…) – are not announced correctly by screen readers. When writing alternative text descriptions, write out the words “first, second, third, fourth…”.
- In cases where double or triple-digit numbers are present such as 22nd and 158th, numbers should be written as “twenty-second” and “one hundred and fifty-eighth”.
- Numbers with decimals (3.5) – are read correctly by screen readers. Numbers with decimal points are correctly read without the need to write out the number or decimal point. The number 3.5 is announced as “3 point 5”.
- Roman Numerals – some screen readers may read them incorrectly. For example, Roman numeral 5 which is the letter V is announced as the letter V and not 5. When using Roman numerals in alt text, write it out as “Roman numeral 5” and avoid using the Roman numerical system.
Exception: When students are learning Roman numerals, the description may require special handling to best address the level and context of the content. - Dates – When writing:
- Months – Avoid using abbreviations, write out the whole word.
- Day – Use cardinal numbers instead of ordinal numbers.
- Year – Use a space in the middle of the 4-digit number so screen readers announce the year as we speak it naturally. For example, the year “1968” should be written as “19 68”. This will ensure all screen readers announce it as intended.
Basic Math Symbols
| Symbol | Alternative Text | Guidance |
|---|---|---|
| + | + | use the symbol and not the word plus |
| – | minus negative | 5 minus 2 = 3 negative 2 Use the words minus and negative as appropriate. |
| x | times | |
| ÷ | divided by | |
| / | over, per, divided by | Use “over” and “per” as appropriate. Only use “divided by” for the forward slash character when used for division. |
| = | = | Use the equals symbol except when a math object starts with an equal symbol (e.g., a step in a solution) then use the word “equals”. |
| ( ) | left paren right paren | Use the shortened form instead of writing out the full word. This helps with reducing character counts within the alt text description. |
Subscripts and Superscripts
Prior to December 2023, Pearson advised authors to indicate subscripts and superscripts when describing STEM elements in alternative text. However, moving forward, only denote them when necessary for the user to grasp the equation’s meaning.
When a title comes up for re-edition, STEM elements which include subscripts or superscripts, it is not required to edit previously written descriptions. It is acceptable to maintain the alternative text previously written and follow the “refreshed” guidelines for new alternative text.
The shortened form “sub” and “super” are highly recommended for two main reasons:
- Fosters brevity.
- Reduces the alt text character count which is helpful when trying to stay under 255 characters.
In the following examples, subscripts and superscripts are NOT needed to understand the content:
| Math Expression | Alternative Text |
|---|---|
| H2O | H 2 O |
| CH4 | C H 4 |
| x5 | x to the fifth power |
| f-1(x) | f inverse of x |
| d2y / dx2 | d 2 y over d x squared |
| 1s22s22p63s23p2 | 1 s 2, 2 s 2, 2 p 6, 3 s 2, 3 p 2 |
Examples when subscripts/superscripts are NEEDED in alt text to avoid ambiguity:
| Expression | Alternative Text |
|---|---|
| P1V1=P2V2 | P sub 1 V sub 1 = P sub 2 V sub 2 |
| z1 = r1(cos θ1 + i sin θ1) | z sub 1 equals r sub 1 left paren cosine theta sub 1 plus i sine theta sub 1 right paren |
| anpn + an-1pn-1 + . . . | a sub n times p to the n power plus a sub n minus 1 baseline p to the n minus 1 power plus ellipsis |
Scientific Notation/Numbers with Powers
| Expression | Alternative Text | Guidance |
|---|---|---|
| 102 | 10 squared | |
| 103 | 10 cubed | |
| 105 | 10 to the fifth power | Using the word “raised” in the description should be avoided since it is known “fifth power” is raised. |
| 10-1 | 10 to the negative first power | |
| 10-2 | 10 to the negative second power | |
| 10-3 | 10 to the negative third power | |
| 2.37 x 102 | 2.37 times 10 squared | |
| 7 x 1022 | 7 times 10 to the twenty-second power | It is grammatically incorrect to use “20 second” as an alt text for “22”. Logically 22 should be written as “twenty second”. |
Mathematical Expressions
| Property/Category | Expression | Alternative Text | Guidance |
|---|---|---|---|
| Boyle’s Law | P1V1 = P1V2 | P sub 1 V sub 1 = P sub 2 V sub 2 | For this mathematical expression, it is necessary to use subscripts and superscripts to avoid ambiguity. The abbreviation “sub” is preferred because it has fewer characters. |
| Charles’ Law | V1/T1=V2/T2 | V sub 1 divided by T sub 1 = V sub 2 divided by T sub 2. | For this mathematical expression, it is necessary to use subscripts and superscripts to avoid ambiguity. The abbreviation “sub” is preferred because it has less characters. |
| Mathematical equation (example 1) | 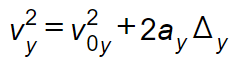 | v sub y squared = v sub 0 y baseline squared plus 2 a sub y delta y | For this mathematical expression, it is necessary to use subscripts and superscripts to avoid ambiguity. Baseline is used after the description of the subscripts whenever there is more than one subscript character present for any term for better clarity. Whenever there is only one subscript character associated with a term, no need to use “baseline” after the description of the subscripts. |
| Mathematical equation (example 2) | 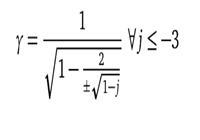 | Gamma = StartFrac 1 over StartRoot 1 minus StartFrac 2 over plus or minus StartRoot 1 minus j EndRoot EndFrac EndRoot EndFrac for all j less than or equal to negative 3. | |
| Mathematical equation (example 3) | 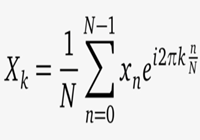 | X sub k = StartFrac 1 over Uppercase N EndFrac times summation from n equals 0 to uppercase N minus 1 of x sub n times e to the i 2 pi k times StartFrac n over uppercase N EndFrac power. | |
| Fractions (Example 1) | 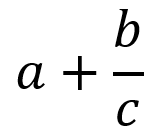 | a + StartFrac b over c EndFrac | Note: a + b over c would be ambiguous and could be interpreted as (a + b)/c or a + (b/c) |
| Fractions (Example 2) | 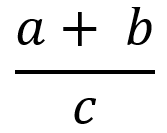 | StartFrac a + b over c EndFrac | Note: a + b over c would be ambiguous and could be interpreted as (a + b)/c or a + (b/c) |
| Logarithms | log4 x | log base 4 of x | |
| Limits | 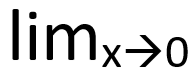 | the limit as x approaches zero | Limits are written with “lim” on the baseline and |
Other Mathematical Notation
| Property/Category | Expression | Alternative Text | Guidance |
|---|---|---|---|
| Line labels or calculator notation | L1 or X1 | L sub 1 or X sub 1 | |
| Number base systems | 3245 or 324five | 3 2 4 base 5 | not three hundred twenty-four |
| Matrix elements | a32 | a sub 3 2 | not thirty-two (3 represents the row number and 2 represents the column number) |
| Exponential function | ex | e to the x | usually omit “raised” |
| Exponential function | 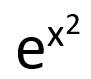 | e to the x squared | usually omit “raised” |
| Inverse function | f -1(x) | f inverse of x | |
| Inverse trig function | sin-1x | inverse sine of x | The word inverse is typically stated before the trigonometric function. |
Derivatives
| Property/Category | Expression | Alternative Text | Guidance |
|---|---|---|---|
| Derivatives (prime notation) | y′, y″, y‴ | y prime, y double prime, y triple prime | |
| Derivatives (n notation) | f (n), f (5) | enth derivative of f, fifth derivative of f | |
| Second derivatives | d2y / dx2 | d two y over d x squared | |
| Second order partial derivatives | ∂2f / ∂y∂x | Partial 2 f over partial y partial x |
Molecular Formulae
| Expression | Alternative Text | Guidance |
|---|---|---|
| H2O | H 2 0 | Omit the word “subscript” to mirror how it is pronounced naturally in speaking. Place a space between each letter/number. |
| CH4 | C H 4 | Omit the word “subscript” to mirror how it is pronounced naturally in speaking. Place a space between each letter/number. |
| Al2(SO4)3 | A l 2 left paren S O 4 right paren sub 3 | Use subscript and parenthesis abbreviations to clarify what subscript 3 is modifying. |
| (NH4)2SO4 | Left paren N H 4 right paren sub 2 S O 4 | Here it is necessary to use subscript and parenthesis abbreviations, so the expression is not ambiguous. |
| H2SO4 | H 2 S O 4 | |
| CH3CH2CH3 | C H 3 C H 2 C H 3 | |
| CH3(CH2)3CH3 | C H 3 left paren C H 2 right paren sub 3 C H 3 | |
| SO42- | S O 4 2 minus | For ions and molecular formulae, charges appear as superscript numbers followed by a plus or minus sign. It is understood that numbers following an element symbol are subscript, and charges are superscript. In this example, it is clear which symbols represent the charge. Thus, superscript is not needed and can be omitted. |
| O2- O2– | O super 2 minus O 2 super minus | When writing alt text add superscript when there is ambiguity. Here you need to indicate the superscript position. If not, the oxide and superoxide ions would both be read as “O 2 minus”. |
| Cl– | C l super minus | When writing alt text add superscript to ions with charges of plus or minus 1, which are represented by a superscript plus or minus symbol only. In this example the chloride ion has a charge of minus 1. So, the ion symbol Cl- would be read aloud as “C l minus” but when writing alt text indicate the “super” position to avoid ambiguity. |
Units of the Properties
| Property/Category | Expression | Alternative Text | Guidance |
|---|---|---|---|
| Energy/enthalpy | KJ mol-1 | kilojoules per mole | Use the elaborate description of units to avoid ambiguity that would arise due to the use of alphabets, since an alphabet may represent units for different properties. For ex., kelvin is represented by K and kilo is represented by k. Similarly, “m” may represent mass or meter. |
| Entropy | J mol-1 k-1 | joules per mole per kelvin | It is preferable to use the elaborate description of units to avoid ambiguity that would arise due to the use of alphabets, since an alphabet may represent units for different properties. For ex., kelvin is represented by K and kilo is represented by k. Similarly, “m” may represent mass or meter. |
| First order rate constant | s-1 | per second | It is preferable to use the elaborate description of units to avoid ambiguity that would arise due to the use of alphabets, since an alphabet may represent units for different properties. For ex., kelvin is represented by K and kilo is represented by k. Similarly, “m” may represent mass or meter. |
| Temperature-Kelvin scale | K | Kelvin | It is preferable to use the elaborate description of units to avoid ambiguity that would arise due to the use of alphabets, since an alphabet may represent units for different properties. For ex., kelvin is represented by K and kilo is represented by k. Similarly, “m” may represent mass or meter. |
| Density | kg m-3 | kilogram per cubic meter | It is preferable to use the elaborate description of units to avoid ambiguity that would arise due to the use of alphabets, since an alphabet may represent units for different properties. For ex., kelvin is represented by K and kilo is represented by k. Similarly, “m” may represent mass or meter. |
| Complex Derived Unit – Watt | kg m2 s-3 or 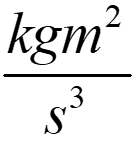 | Kilogram meters squared per second cubed | “Derived” units are formed by combining “base” units such as kilograms, meters, and seconds. This example shows the derived unit we usually refer to as a “watt.” In physics calculations, we must often write out derived units in terms of their base units, so that the base units can be recombined or canceled. There are two basic rules for writing out derived or composite units in terms of their base units. Rule 1: If the derived unit includes a sequence of more than one base unit, the number (singular, plural) of the last base unit should match the associated value. This is true even if the last base unit has an exponent. For example, the unit for moment of inertia is “kilogram meter squared.” The base unit “meter” is last. So, this unit will be singular or plural depending on the associated value. We write “1 kilogram meter squared” and “3 kilogram meters squared.” We do not change “kilogram,” however. If the derived unit is a fraction, this rule only applies to a sequence of base units in the numerator. The units in the denominator should always be singular. Rule 2: If a sequence of base units includes a unit of distance raised to the second or third power, do not use “square” or “cubic” before the unit. For the example in column 2, we write “kilogram meters squared per second cubed” rather than “kilogram square meters per second cubed.” |
| Density | g mL-1 | gram per milliliter | It is preferable to use the elaborate description of units to avoid ambiguity that would arise due to the use of alphabets, since an alphabet may represent units for different properties. For ex., kelvin is represented by K and kilo is represented by k. Similarly, “m” may represent mass or meter. |
| Density | g cm-3 | gram per cubic centimeter | It is preferable to use the elaborate description of units to avoid ambiguity that would arise due to the use of alphabets, since an alphabet may represent units for different properties. For ex., kelvin is represented by K and kilo is represented by k. Similarly, “m” may represent mass or meter. |
| Specific Conductance/conductivity | Sm-1 | Siemens meter inverse | It is preferable to use the elaborate description of units to avoid ambiguity that would arise due to the use of alphabets, since an alphabet may represent units for different properties. For ex., kelvin is represented by K and kilo is represented by k. Similarly, “m” may represent mass or meter. |
| Acceleration | ms-2 | meter per second squared | It is preferable to use the elaborate description of units to avoid ambiguity that would arise due to the use of alphabets, since an alphabet may represent units for different properties. For ex., kelvin is represented by K and kilo is represented by k. Similarly, “m” may represent mass or meter. |
Dated: 2024-01-17

